Направления исследований
Основные направления исследования научного коллектива в 2024 году:
Проект 1. The sample complexity of ERM for stochastic convex-concave Saddle-Point-Problems.
Для задач выпуклой стохастической оптимизации подход, связанный с минимизацией эмпирического риска довольно хорошо сейчас уже проработан. В частности, получены оценки вероятностей больших отклонений, размерность выделена в отдельное слагаемое (показано, что требуется разное число сэмплов для задач равномерной аппроксимации функции риска эмпирическим риском и для задачи обоснования принципа минимизации эмпирического риска), рассмотрены различные условия роста в решении:
Shalev-Shwartz S. et al. Stochastic Convex Optimization //COLT. – 2009. – Т. 2. – №. 4.

Для седловых задач результаты значительно скромнее:
В частности, нет разделения задач равномерной аппроксимации функции риска эмпирическим риском и задачи обоснования принципа минмакса эмпирического риска (см. Carmon D., Yehudayoff A., Livni R.).
Задача заключается в перенесении того, что уже было сделано для выпуклой стох. оптимизации на выпукло-вогнутые стох. минмакс задач. В том числе для задач с неодинаковыми константами сильной выпуклости и вогнутости, и в том числе в плане более тонких результатов о сходимости всяких процедур типа SGD, GD, их ранней остановки и т.п., например:
Куратор – Виталий Кондратюк.
Проект 2. Безградиентные методы для задач стохастической оптимизации со скрытой выпуклой структурой.
Основная статья тут:
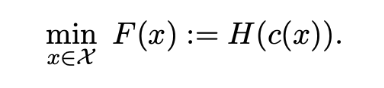
Функция H(x) выпуклая, а функция c(x) удовлетворяет условию:
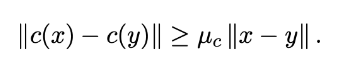
Несложно проверить, что эта задача может рассматриваться как задача в условиях градиентного доминирования (Поляка–Лежанского–Лоясиевича) или в общем (негладком) случае Курдюка–Лоясиевича, см. Proposition 2 Fatkhullin I., He N., Hu Y.. С другой стороны, также недавно вопрос о безградиентных методах для задач стохастической оптимизации (и их седловых версий) в условиях Поляка–Лоясиевича довольно подробно исследовался, см., например:
и цитируемую там литературу.
Было бы интересно сопоставить эти работы и получить максимально сильные результаты о сходимости безградиентных методов для задач стохастической оптимизации (и их седловых обобщений, в том числе с неодинаковыми константами сильной выпуклости и вогнутости).
Куратор – Александр Лобанов.
Проект 3. Безградиентные методы для задач стохастической оптимизации и седловых задач с ограничениями.
Тема безградиентных методов для седловых задач в литературе уже довольно часто встречалась, см., например, наиболее свежую работу
и цитируемую там литературу. Большинство современных подходов к получению такого типа результатов базируется на схеме
Gasnikov A. et al. The power of first-order smooth optimization for black-box non-smooth problems //arXiv preprint arXiv:2201.12289. – 2022.
в основе которой лежит правильно подобранный (батчированный) метод стохастической оптимизации, на основе которого и строится искомый безградиентный. В частности, для седловых задач (в том числе с ограничениями) в качестве базовых методов можно, например, рассматривать методы из работ
конкретно для этих двух статей Metelev D. et al. и Zhang X., Aybat N. S., Gürbüzbalaban M. нужное обобщение сделано в Gasnikov A. et al. и здесь мы это привели, чтобы лучше понять о чем идет речь; впрочем, в Gasnikov A. et al. есть ограничение на билинейность седловой части, от которой было бы интересно избавиться)
Первая задача заключается в получении результатов для седловых задач стохастической оптимизации на базе Metelev D. et al. и Boob D., Deng Q. с помощью техники Gasnikov A. et al.
Более сложной задачей является обобщения тонкого детерминированного результата из важной (но незаслуженно мало цитируемой) статьи
на случай стохастического оракула (то есть на задачи стохастической оптимизации, можно заодно и на седловые задачи и ВН с ограничениями). По-видимому, это довольно тонкий результат, впрочем, основное наблюдение данной статьи такое


Это наблюдение фактически синонимично теории модельной общности, развитой в цикле работ:
Гасников А.В. Пособие МЦНМО, глава 3
Может понадобиться аналогия с тем, как получено обобщение на случай стохастической оптимизации
Это должно позволить существенно уточнить (улучшить) современные SOTA результаты по безградиентной стохастической оптимизации для задач с ограничениями
Куратор – Александр Лобанов.
Проект 4. Безградиентные адаптивные методы для задач стохастической оптимизации.
Первой задачей является добавление адаптивного батчирования в схемы (также интересно было бы понять по анализу списка литературы в этих статьях, есть ли аналогичные результаты для седловых задач и ВН)
Например, в статье Rodomanov A. et al. Universal… стр. 12
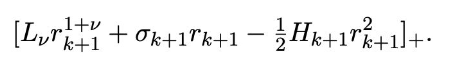
можно так выбирать размер батча, чтобы второе слагаемое стало не больше половины от третьего или половины первого (того, что больше). На практике это можно контролировать, используя вычислимое k (увеличивая размер батча и наблюдая стабилизацию k) и неравенство
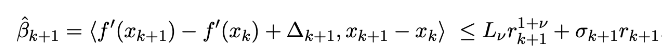
На практике это должно работать, но для теоретического обоснования требуется докрутрка… Возможно полной адаптивности не получится и в оценку будут входить оценки сверху и снизу на какие-то параметры, наподобие
что, скорее всего, будет подразумевать логарифмическое число рестартов по этим параметрам подобно Attia A., Koren T.. Интересно обратить внимание на Теорему 6 из этой статьи. Эта нижняя оценка указывает плату за адаптивность. Более системно этот вопрос проработан в статье:
исследующей негладкие постановки задачи (кажется, все это полезно было бы перенести и на случай ускоренных методов, то есть гладкий случай). Полезно также упомянуть работу, в которой описываются как можно достигать нижних оценок:
Khaled A., Jin C. Tuning-Free Stochastic Optimization //arXiv preprint arXiv:2402.07793. – 2024.
Все три статьи Attia A., Koren T., Carmon Y., Hinder O., Khaled A., Jin C., более менее, об одном и том же. Об адаптивных методах стохастической минимизации без ускорения, что, например, может быть связано с онлайновостью, негладкостью (получены нижние и верхние оценки).
Второй задачей является внедрение в общую схему получения безградиентных методов, упомянутую ранее в проекте 3
описанных выше пробатчинных вариантов адаптивных ускоренных методов. С точностью до адаптивности по размеру шага. По последнему, возможно, понадобятся рестарты (см. выше).
Кураторы – Александр Лобанов, Петр Остроухов, Павел Двуреченский
Проект 5. Лучшие оценки для ускоренных методов и их безградиентных вариантов в условиях повышенной гладкости.
Задачи квадратичной оптимизации в зависимости от спектральных свойств можно решать быстрее чем обычным ускоренным методом
Выступление Фабиента Педрегозы и его статьи по теме:
https://www.mathnet.ru/php/seminars.phtml?option_lang=rus&presentid=34056
Собственно, это привело к появлению вот таких двух работ
Результаты обеих работ обобщаются на случай общих задач выпуклой оптимизации (в условиях повышенной гладкости), путем сведения с помощью метода Монтейро–Свайтера (оптимального метода второго порядка). Идея очень простая – каждая подзадача в таком методе сводится к квадртатичной (по типу метода Ньютона), последняя уже решается с учетом спектральных свойств. Собственно, естественная идея заменить метод Монтейро–Свайтера оптимальным методом третьего порядка имплементируемого как метод второго порядка (идея Ю.Е. Нестерова). В целом про все это можно посмотреть вот тут
и цитируемой тут литературе.
Также интересно бы было обобщить результаты работы Yue P. et al. и Liu Y. et al. на седловые постановки задач.
Интересно бы было все это сопоставить и с анализом в среднем:
Кураторы – Дмитрий Камзолов, Александр Рогозин
Проект 6. Сходимость по критерию нормы градиента для задач стохастической федеративной оптимизации.
Сходимость по норме градиента часто требует отдельно более тонкой техники, если хочется получить правильные оценки, см., например:
Гасников А.В. Пособие МЦНМО Замечание 5.3 и цитированная там литература.
Дополнительные сложности появляются для задач стохастической оптимизации:
Однако в литературе в последние годы популярны не только обычные седловые задачи (в том числе стохастические), но и задачи с разными константами сильной выпуклости/вогнутости. Попробуйте обобщить результаты статьи Chen L., Luo L. на такой случай. Полезно будет познакомиться с обзором про стохастические методы решения ВН и седловых задач
Куратор – Екатерина Бородич
Проект 7. Распределенная оптитмизация в условиях схожести слагаемых. Оптимальные методы по числу раундов коммуникаций, коммуникационной сложности и общему числу вызовов оракула.
Относительно недавно появилась вот такая статья, в которой исследуется методы распределенной оптимизации в условиях схожести слагаемых (постановка задачи оптимизации вида суммы)
На базе этой статьи предлагается попробовать сделать оптимальный метод по всем трем критериям (число раундов коммуникации, коммуникационно сложности и общему числу вызовов оракула) за счет батчирования; возможно понадобится сочетание работы Kovalev D. et al. Optimal gradient sliding and its application to optimal distributed optimization under similarity //Advances in Neural Information Processing Systems. – 2022. – Т. 35. – С. 33494-33507 трюка редукции дисперсии и батчирования. Помочь в этом может то, как это было сделано для седловых задач вот тут:
Zhou Q., Ye H., Luo L. Near-Optimal Distributed Minimax Optimization under the Second-Order Similarity //arXiv preprint arXiv:2405.16126. – 2024. (эту работу, кажется, можно обобщить на случай разных констант сильной выпуклости/вогнутости с помощью работы Tian Y. et al. Acceleration in distributed optimization under similarity //International Conference on Artificial Intelligence and Statistics. – PMLR, 2022. – С. 5721-5756, интересно ее было бы обобщить и на случай неевклидовой нормы Beznosikov A. et al. Bregman Proximal Method for Efficient Communications under Similarity //arXiv preprint arXiv:2311.06953. – 2023, для этого может понадобится вот такого типа результаты о батчировании в неевклидовой норме Pichugin A. et al. Optimal analysis of method with batching for monotone stochastic finite-sum variational inequalities //arXiv preprint arXiv:2401.07858. – 2024)
Отметим, что в работе Lin D. et al. не предполагается выпуклость отдельных слагаемых (нужна выпуклость суммы). Этим и обусловлена полученная оценка коммуникационной сложности и оракульной:
В действительности, если дополнительно известно, что в каждом узле, в свою очередь, находится функция вида суммы, то интересно бы было посмотреть, как в таком случае можно было бы дополнительно редуцировать оракульную сложность и коммуникационную (где теперь уже эти сложности понимается в смысле подсчета/перессылки градиентов отдельных слагаемых в каждом узле). Помочь тут могут вот эти статьи:
Кураторы – Александр Безносиков, Дарина Двинских
Проект 8. Сходимость в условиях перепараметризации.
В недавней статье
получены условия сходимости ускоренных методов (с батчированием) в условии перепараметризации (дисперсия входит в оценку только в решении, то есть если в самом решении дисперсия мала, то и вклад шума мал). Совсем недавно такого типа результаты были получены и для безградиентных методов
и для адаптивных:
Возникает естественный вопрос, в какой степени все это переносится на федеративную оптимизацию:
Куратор – Александр Лобанов.
Проект 9. Стохастическая децентрализованная оптимизация на меняющихся графах для негладких задач выпуклой оптимизации и выпукло-вогнутых седловых задач.
В недавней статье:
предложен метод решения негладких задач децентрализованной выпуклой оптимизации на меняющихся графов. Кажется, что аналогичные оценки должны быть и для задач стохастических оптимизации (также в условиях негладкости) и их седловых версий. Во всяком случае так получается для задач на не меняющихся графах (возможно, тут можно попробовать сделать как-то по аналогии)
Куратор – Екатерина Бородич
Направления исследований 2022 года научного коллектива:
Распределенная оптимизация
Recent theoretical advances in decentralized distributed convex optimization
Decentralized optimization over time-varying graphs
В частности, в условиях симиларити и с редукцией дисперсии: Optimal Gradient Sliding and its Application to Distributed Optimization Under Similarity
Optimal Algorithms for Decentralized Stochastic Variational Inequalities
Ниже описаны проекты, которыми можно заниматься по данному направлению (проектов намного больше, здесь приведено лишь несколько примеров):
Оптимальные оценки для Вариационных Неравенств (ВН) в архитектуре Federated Learning (FL)
В качестве задачи, прежде всего, рекомендуется разобраться вот с этой статьей: The Min-Max Complexity of Distributed Stochastic Convex Optimization with Intermittent Communication. Особенно, в части получения формул (12) и (13). По сути то, о чем тут идет речь, есть ускоренный метод с батчами, просто с разным размером батча (1 и максимально возможным, при котором от батчирования есть эффект).
Собственно, задачей является перенесение результатов статьи The Min-Max Complexity of Distributed Stochastic Convex Optimization with Intermittent Communication в части оптимальных методов на седловые задачи и ВН на базе метода из работы Solving variational inequalities with stochastic mirror-prox algorithm и его пробатченного варианта.
Более тонкой задачей является получение нижней оценки в архитектуре FL для ВН наподобие того, как это было сделано в статье The Min-Max Complexity of Distributed Stochastic Convex Optimization with Intermittent Communication. В других архитектурах это сделано, например, в работе Distributed saddle-point problems: lower bounds, near-optimal and robust algorithms.
В случае седловых билинейных задач (с квадратичными композитами) и даже более общего класса ВН с линейным векторным полем, кажется, что в случае стох. постановок может иметь место результаты типа Is Local SGD Better than Minibatch SGD? (Section 3). Было бы здорово это проверить.
Оптимальные оценки для задач выпуклой оптимизации в условиях интерполяции в архитектуре FL
В 2021 году вышла статья, в которой впервые показывается, как ускоренные методы уживаются с условиями интерполяции в плане батчирования: An Even More Optimal Stochastic Optimization Algorithm: Minibatching and Interpolation Learning
Однако, этого пока не было сделано в FL архитектуре. Зато было сделано (оптимальные методы для задач гладкой выпуклой оптимизации в архитектуре FL) без условий интерполяции: The Min-Max Complexity of Distributed Stochastic Convex Optimization with Intermittent Communication. То есть задача — поженить эти две работы.
Релевантная статья по теме: Faster Convergence of Local SGD for Over-Parameterized Models
Редукция дисперсии, проксимальные оболочки, симиларити в неевклидовом прокс сетапе с приложением к задаче поиска барицентра Васерштейна.
В работе Дмитрия Ковалева Optimal Algorithms for Decentralized Stochastic Variational Inequalities от 2022 года был предложен оптимальный децентрализованный алгоритм решения безусловных седловых задач (сильно выпукло-вогнутых) с редукцией дисперсии. Как известно, задача поиска барицентра Васерштейна (см. Decentralized Distributed Optimization for Saddle Point Problems, а также Numerical Methods for Large-Scale Optimal Transport) может быть сведена как раз к седловой задаче, причем решать такую задачу удобно распределено (в том числе и децентрализованно), в виду больших вычислительных затрат. Причем, на одном узле, естественно, хранить несколько картинок (слагаемых исходной большой суммы).
Таким образом приходим к седловой выпукло-вогнутой задаче децентрализованной оптимизации вида суммы, в которой в каждом узле хранится функция, в свою очередь, имеющая вид суммы функций. Децентрализованные алгоритмы решения таких задач, учитывающие, структуру вида суммы функции, хранящейся в каждом узле, при условии, что есть возможность обращаться к каждому из слагаемых этой суммы отдельно (например, есть возможность вычислять градиент каждого слагаемого), называются децентрализованными методами с редукцией дисперсии. Результаты статьи Ковалева и других не подходят для задачи вычисления барицентра Васерштейна (ВБВ) сразу по нескольким причинам:
1) у задачи ВБВ в седловом представлении нет сильной выпукло-вогнутости (есть просто выпукло-вогнутость, но не сильная);
2) у задачи ВБВ в седловом представлении есть ограничения;
3) схема статьи Ковалева и др. предполагает, что по max и по min переменным выбирается евклидова норма в оптимальном методе. В задаче ВБВ (как следует из работы Рогозина и других) по группе min переменных выгодно выбирать 1-норму (поскольку есть симплексные ограничения на min переменные).
Планируется развить результаты статьи Ковалева и других на более общий класс задач выпукло-вогнутой оптимизации с ограничениями и не обязательно евклидовыми прокс-структурами, чтобы можно было применить эти результаты к задаче ВБВ в седловом представлении.
Отметим, что редукция дисперсии в неевклидовом прокс-сетапе (но нераспределенном) ранее прорабатывалась в работе Stochastic Variance Reduction for Variational Inequality Methods для седловых задач и ВН, а в материале A unified variance-reduced accelerated gradient method for convex optimization для обычной оптимизации.
В работе Александра Безносикова Distributed Saddle-Point Problems Under Data Similarity (см. также Optimal Gradient Sliding and its Application to Distributed Optimization Under Similarity — вариант без лишнего лоагрифма, правда, в централизованном случае) был предложен эффективный распределенный (в том числе и децентрализованный) способ решения безусловных сильно выпукло-вогнутых седловых задач вида суммы, в которых слагаемые являются близкими функциями. Как уже отмечалось выше, в задаче ВБВ в седловом представлении слагаемые имеют вид суммы функций. Если задача ВБВ пришла из анализа данных и каждая картинка/мера (барицентр которых ищется) независимо сэмплирована из одного и того же распределения, то в каждом узле хранится сумма статистически независимых функций, сэмплированных из одного и того же распределения. Это означает, что функции, хранящиеся в узлах, статистически близки (степень близости обратно пропорционально корню из числа слагаемых, хранящихся в узле).
Таким образом, можно по-другому обыграть структуру задачи и вместо редукции дисперсии (которая максимально экономит оракульные вызовы в узлах, то есть число вычислений градиентов слагаемых в каждом узле, но не экономит число коммуникаций между узлами) использовать схожесть функций, хранящихся в узлах, и существенно сэкономить в числе коммуникаций. К сожалению, прямое приложение результатов статьи Безносикова и др. к задаче вычисления ВБВ в седловом представлении не работает ровно по тем же трем причинам, что и были указаны выше. Планируется развить результаты статьи Безносикова и др. на более общий класс задач выпукло-вогнутой оптимизации с ограничениями и не обязательно евклидовыми прокс-структурами, чтобы можно было применить эти результаты к задаче ВБВ в седловом представлении.
В обоих сюжетах наиболее сложным местом представляется обобщение на неевклидовы прокс-структуры и наличие ограничений. Это все потребуется существенно новых идей и отличной техники. Дело в том, что в статьях Ковалева и др. и Безносикова и др. существенным образом использовалась евклидовость нормы. Рассуждения этих статей уже не пройдут для случая общей нормы.
Тензорные методы их приложения
Exploiting higher-order derivatives in convex optimization methods
В данном направлении планируется развивать идею, что задачи квадратичной стохастической оптимизации в архитектуре федеративного обучения очень эффективно могут быть решены в смысле необходимого числа коммуникаций. А для тензорных методов вспомогательная задача, которую нужно решать на каждой итерации, похожа на задачу, которую нужно решать на итерации метода Ньютона, стало быть, является квадратичной. Таким образом, есть надежда сократить число коммуникаций при решении задач стохастической распределенной оптимизации тензорными методами.
Отметим, что в 2022 году в этой области сотрудниками лаборатории были получены оптимальные тензорные методы (без лишних логарифмов в оценках сложности): The first optimal acceleration of high-order methods in smooth convex optimization. Однако открытым остается много вопросов, связанных с таким подходом. Прямо-двойственный ли такой метод? Можно ли на его основе построить пробатченный стохастический вариант и т.п.
Безградиентные методы оптимизации
An accelerated method for derivative-free smooth stochastic convex optimization
One-Point Gradient-Free Methods for Smooth and Non-Smooth Saddle-Point Problems
The Power of First-Order Smooth Optimization for Black-Box Non-Smooth Problems
Gradient-Free Optimization for Non-Smooth Saddle Point Problems under Adversarial Noise
Randomized gradient-free methods in convex optimization
Последние исследования в этой области сосредотачиваются не только на получении методов с оптимальными оценками оракульных вызовов, но и методов с оптимальными оценками числа последовательных итераций и методов, наиболее робастных к уровню неслучайного шума (враждебного) в значении функции. Часто это одни и те же методы, оптимальные сразу по всем критериям.
Несмотря на то, что прогресс последнего времени тут довольно большой, по-прежнему остаются вопросы, на которые ответы не известны. Например, для гладких задач неизвестны нижние оценки на максимально допустимый уровень (враждебного) шума, при котором можно решить задачу с заданной точностью. Также неизвестны в общем случае оценки вероятностей больших уклонений для задач стохастической оптимизации с субгауссовским шумом, но не евклидовым прокс-сетапом. А с учетом того, что способы формирования стохастической модели градиента на базе вычисленных значений функции могут быть разными ( Безградиентные прокc-методы с неточным оракулом для негладких задач выпуклой стохастической оптимизации на симплексе, A gradient estimator via L1-randomization for online zero-order optimization with two point feedback, Randomized gradient-free methods in convex optimization), дополнительно возникает задача изучения разных рандомизаций с целью выявления наилучшего по перечисленным выше критериям.
Структурная минимизация
Ускоренные методы для седловых задач
On Accelerated Methods for Saddle-Point Problems with Composite Structure
The First Optimal Algorithm for Smooth and Strongly-Convex-Strongly-Concave Minimax Optimization
В обычной минимизации принято описывать целевую функцию (как представителя некоторого большого класса функций) константами, которые характеризуют поведение функции как функции всех своих аргументов. На самом деле, во многих приложениях (особенно при решении седловых задач) естественным образом выделяются разные блоки переменных, по которым свойства целевой функции существенно разные. Например, это проявляется в многостадийных моделях транспортных потоков при поиске равновесий.
Конечно, можно ориентироваться на худшие константы и использовать известные методы, но насколько можно выиграть от использования такой асимметричной (блочной) структуры? Частично ответ на этот вопрос дают покомпонентные методы. Однако в общем случае вопрос по-прежнему открыт. В последнее время довольно много продвижений было в данном направлении по части седловых задач с разными константами сильно выпуклости и сильно вогнутости, а также разных констант Липшица градиента. Однако, для задач со структурой min min результатов уже заметно меньше.
Более того, и для min max и для min min задач по-прежнему открытыми являются вопросы о нижних оценках. В частности, для задач малоразмерной выпуклой оптимизации нижние оценки получаются с помощью сопротивляющегося оракула https://www2.isye.gatech.edu/~nemirovs/Lect_EMCO.pdf (3 Methods with linear convergence, II, но начать лучше прямо с самого первого раздела Lecture 1 — на одномерном случае все понятнее).
В то время как для задач большой размерности — c помощью «худшей в мире функции» — см., например, указания к упражнениям 1.3 и 2.1 пособия МЦНМО, можно найти на ресурсе Методы Оптимизации. МФТИ. В работе «Решение сильно выпукло-вогнутых композитных седловых задач с небольшой размерностью одной из групп переменных» исследуются задачи min max, в которых одна из групп min переменных имеет небольшую размерность, а другая группа, напротив, большую. Получены верхние оценки.
Интересно было бы попробовать получить нижние оценки путем комбинации двух конструкций. Кажется, что в математическом плане пример построения нижней оценки будет содержать новые интересные идеи. В развитие этого проекта интересно было бы подумать и о нижних оценках для min min задач, в которых по одной из групп переменных (негладких) имеется малая размерность. Верхние оценки имеются в работах « О решении выпуклых min-min задач с гладкостью и сильной выпуклостью по одной из групп переменных и малой размерностью другой» и Solving smooth min-min and min-max problems by mixed oracle algorithms .
Отметим также, что как нижние так и верхние оценки получаются на число вызовов градиентного оракула. Но в задачах с разными блоками переменных можно говорить о разных оракулах. Например в седловой задаче можно говорить о градиенте по min-переменным и градиенте по max-переменным. А если в задаче еще есть и недружественные композиты (градиенты которых в виду «недружественности» также придет считать), то возникает много различных оракулов и, как следствие, много критериев. И говорить об оптимальных методах и нижних оценках в случае нескольких критериев нужно аккуратно. Представляется интересным построение соответствующей теории оптимальных методов для задач со структурой.